Excelで学ぶやさしい統計学では、漠然と数字を表示していました。
しかし、その数字には意味があります。
今回は少し、復習しながら、統計を考えてみます。
みなさんの身近に、統計は存在するのです。
目次
データ分析ツールを利用して、基本統計量を求める
こんにちは。伊川(@naonaoke)です。
今回は、データ分析ツールを利用して、基本統計量を紹介します。
勉強していて、利用していて、データ分析ツールは、本当に便利だと痛感しています。
ここで、重要なのでは、集計と分析は違うということを理解しましょう。
データを集めて計算する⇒これが集計で、関数や、VBAを利用して、データを整形します。
集計されたデータを解析する⇒これが、データ分析です。ここに統計学が、関わります。
統計関数は、統計学の手法を理解していないと使えません。
ほとんどの、Excelの基本書は、集計について記載されています。
しかし、それは、単純な計算です。
Excelは、世界一頭の良い電卓といいましたが、Excelも進化します。
データ分析まで、出来るようになり、クリックだけで、分析結果がでます。
今回も、競馬のデータを利用しますが、ご了承ください。
このブログはこんな人にお勧め
- 統計学を勉強している人
- データ分析ツールを利用したい人
- 集計関数に飽きた人
このブログを、読み終わるころには・・・・
統計学の基礎となる用語を理解できます。また、データ分析ツールにおいて、基本統計量をカンタンに算出できるようになります。
統計関数を利用するのが、馬鹿らしくなるくらいデータ分析ツールは、カンタンに操作できます。
基本統計量とは?
基本統計量とは、データの基本的な特徴を表す値のことで、代表値と散布度に区分できます。
代表値とは、データを代表するような値のことで、例えば、平均値、最大値、最小値などがあります。
散布度とは、データの散らばり度合いを表すような値のことで、例えば、分散、標準偏差などがあります。
基本統計量 作業手順 その1 データベース確認
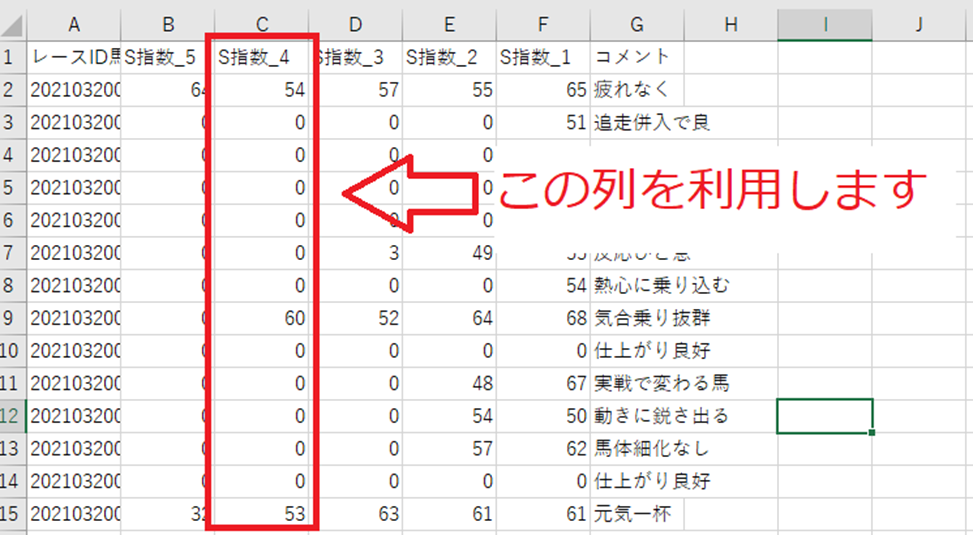
基本統計量 作業手順 その2 データ分析ツール操作手順
データ分析ツールを起動して、基本統計量を選択します。
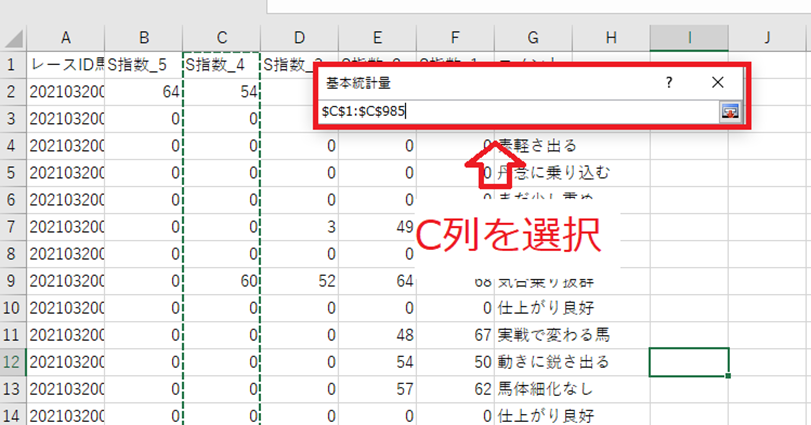
赤枠の中を選択します。
今回は、出力先も設定しました。
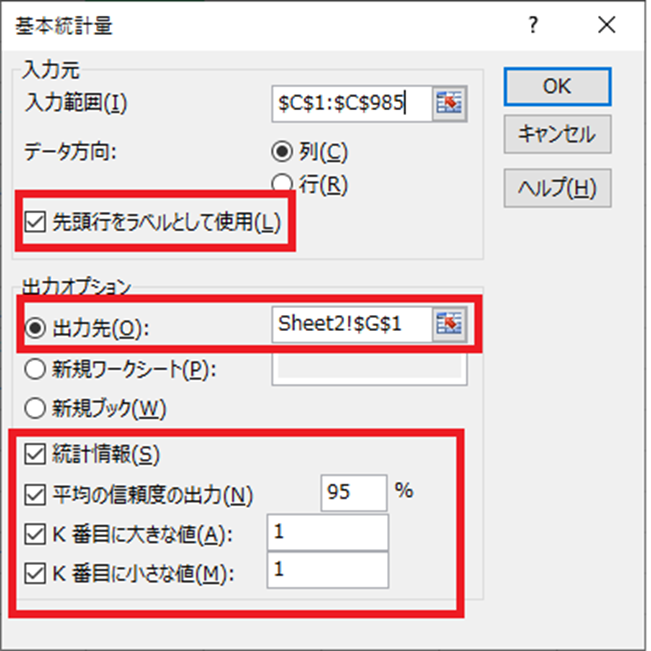
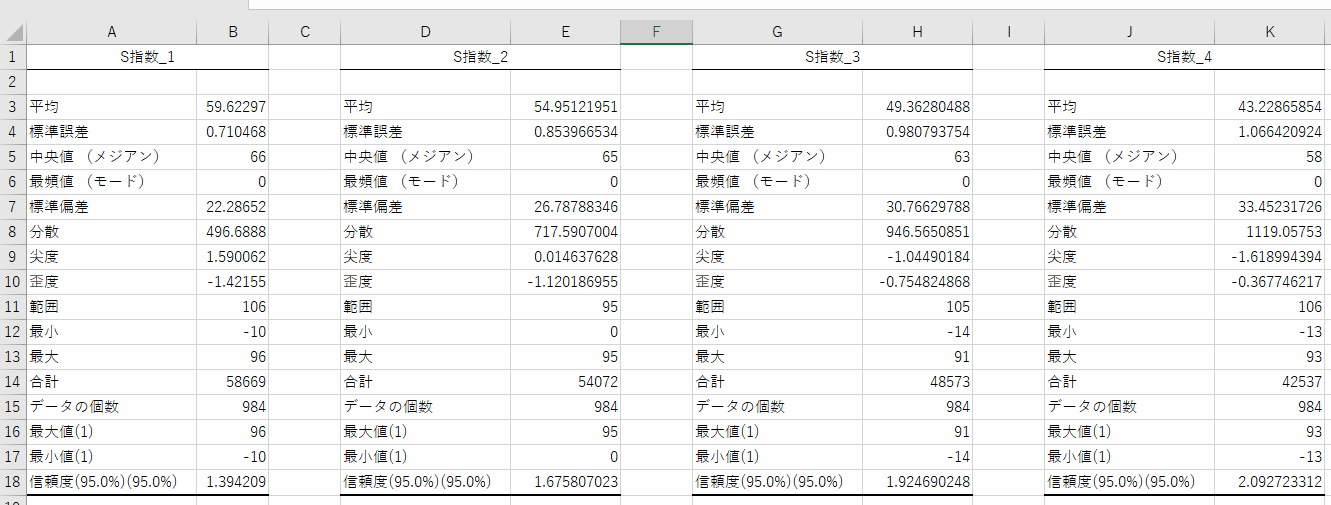
このような分析結果が表示されます。
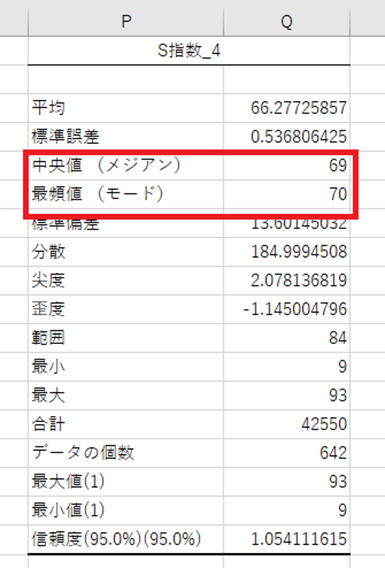
では、S指数_4について説明します。
基本統計量 作業手順 その3 用語解説
平均
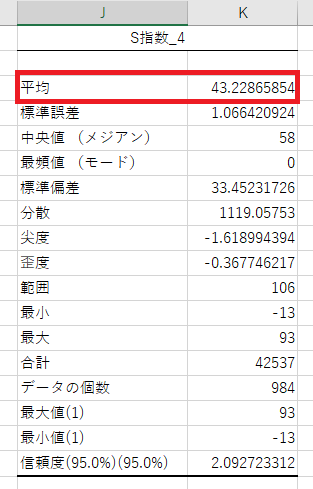
言わずと知れた、平均です。
データの合計を、データ個数で割ったものです。
但し、平均には、相加平均、相乗平均、調和平均の3つがあります。
今回のデータ分析ツールで表示されているのは、相加平均です。(小学校で習う平均です)
最大、最小、範囲
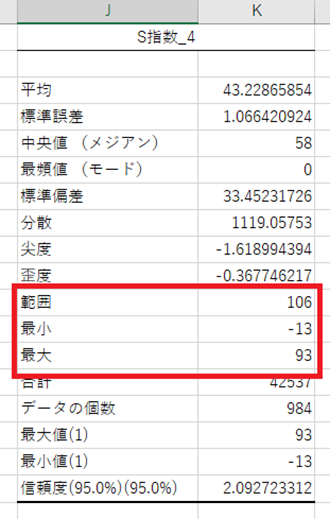
S指数_4の中での、最大値と最小値を表示しています。
範囲というのは、最大値の絶対値と最小値の絶対値を足したものです。
標準偏差を算出する前の、簡易的なバラツキを確認するために使われます。
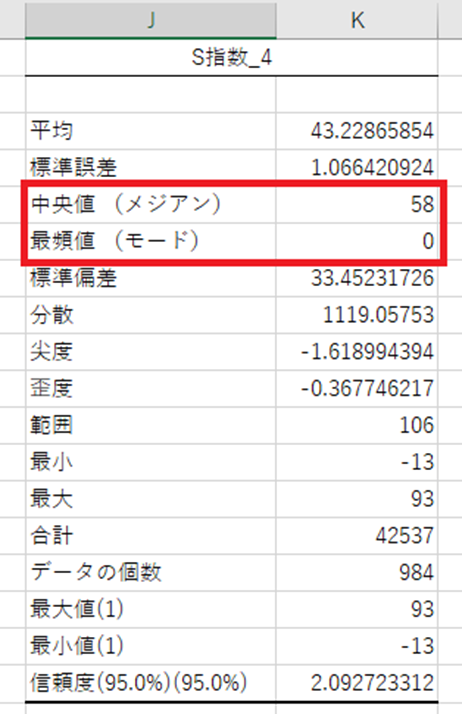
中央値 最頻値
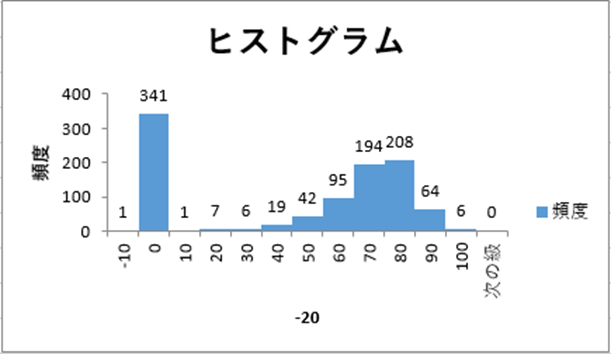
ヒストグラムを描くと上のようになります。
競馬なので、綺麗なグラフが描けません。
便宜上、0を除いたブラフを描きます。
中央値 最頻値(0を除くバージョン)
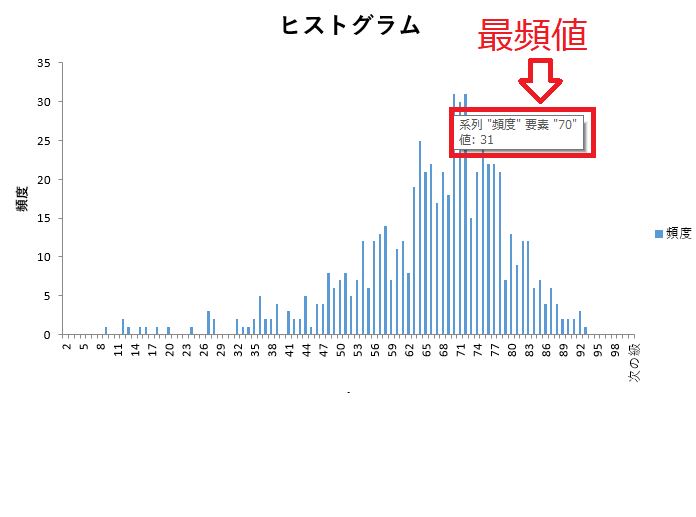
最頻値は、データの中で、最も、出現した値です。
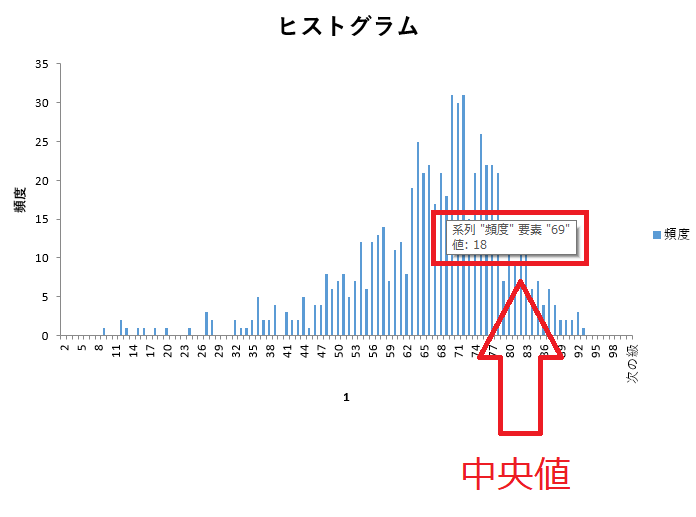
集まったデータの個数が奇数の場合は、小さい順に並び変えた時の真ん中のデータが中央値になります。
集まったデータの個数が偶数の場合は、小さい順に並び変えた時の真ん中2つのデータを平均したものを中央値になります。
例えば、データのうち1つだけめちゃくちゃ大きな値だと、平均は大きく変化しますが、中央値はそれほど変化しません。
このように、中央値は、平均と違い、外れ値(他のデータと大きく外れた値)の影響を受けづらいメリットがあります。
国民の平均年収は、平均値で算出しないで、中央値、または、最頻値で報道すべきなのです。
標準偏差 分散
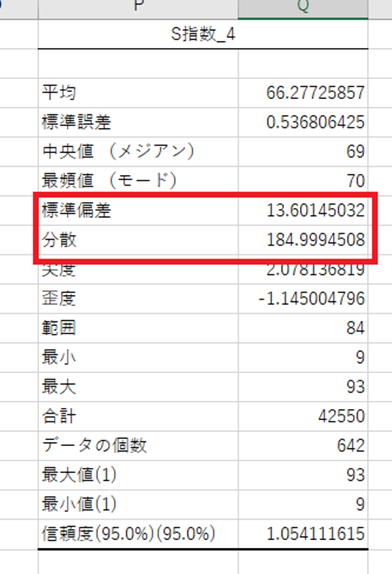
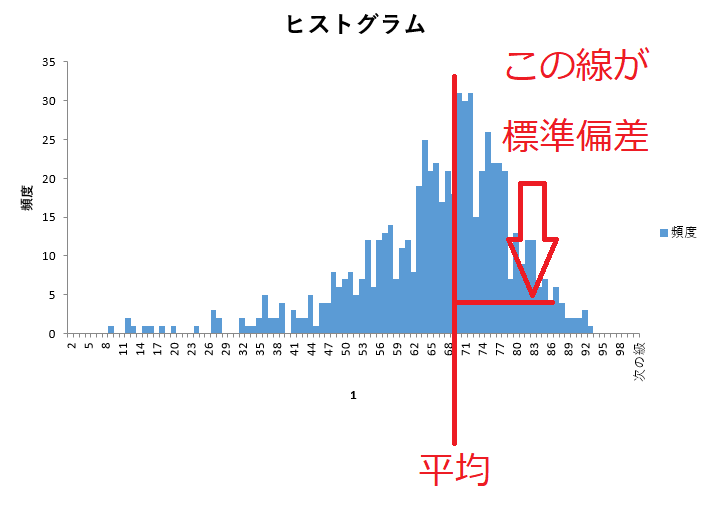
データのバラツキを計測すると、すべて0になります。
よって、すべてのデータの平均と、差を2乗します。
※この説明は、長くなるので、割愛します。
この数字が分散です。
その分散を用いて求めるのが、標準偏差です。
つまり、平均からどれくらい離れているのかということです。
歪度 尖度
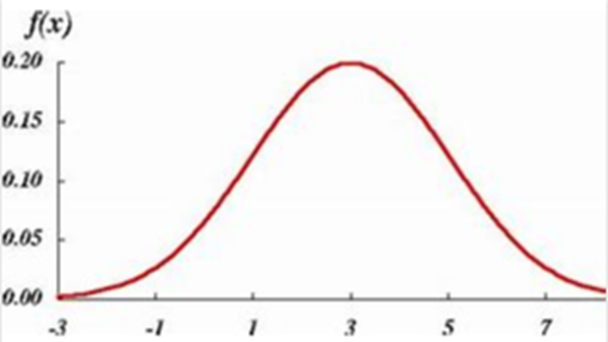
このような図を正規分布と言います。
左右対称になっています。
この時の、歪度、尖度の値は、0になります。
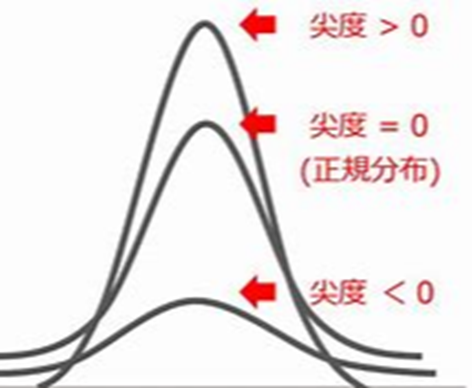
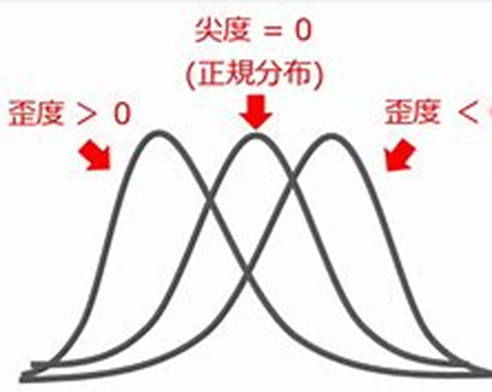
グラフのゆがみ具合を表した数値になります。
標準誤差
選ぶ組み合わせに依って統計量がどの程度ばらつくかを、全ての組み合わせについての標準偏差で表したものをいいます。
例えば、A馬、B馬、C馬の組み合わせと、A馬、B馬、D馬の組み合わせでは、数値が同じでない限り、誤差がでます。
この誤差のことを標準誤差と言います。
合計 データ個数
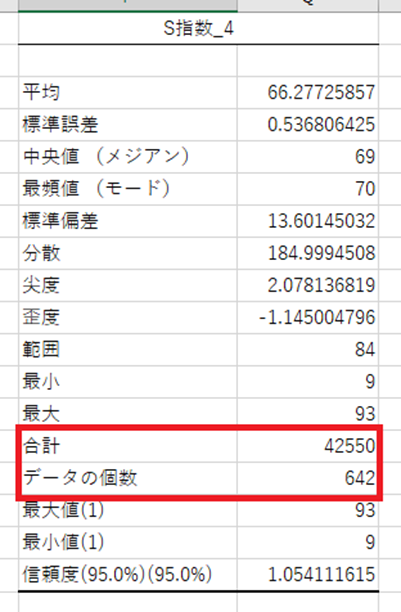
合計は、全数値の合計です。
データ個数は、そのままで、642頭の馬の数値を合計したものです。
最大値 最小値 信頼度
ダイアログボックスの数字を変更します。
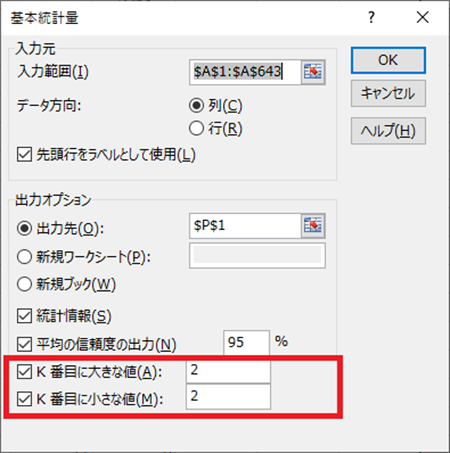
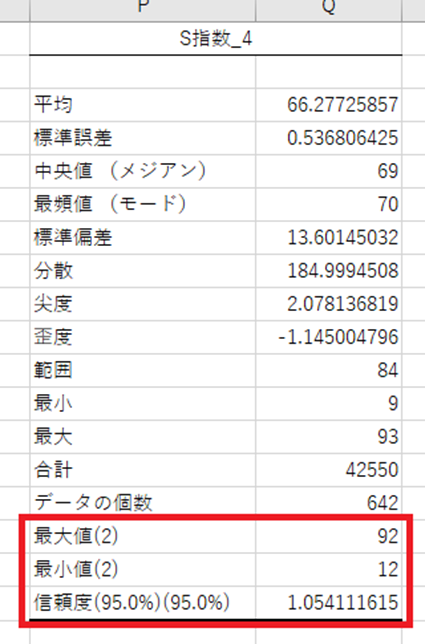
ここに表示されたのは、2番目に大きい数字と、2番目に小さい数字を表示しています。
信頼度に関しては、この数字は、データ分析ツールを使って算出された値は、必ずしも正しいとは言えません。
素朴な疑問
統計を勉強していて、突然、目の前が霧に包まれることがあります。
今回の例でいうと、百位分数で、正確な順位がわかりました。
しかし、その情報から、基本統計量や、正規分布で、全体の何%なのかということをやることが、私は理解できませんでした。
しかも、難しい関数や、難しい言葉が沢山あります。
やっぱり、統計って難しい
今回の例を言うと、
漠然としたデータを、百位分数で使って、1個のデータとして作成した。
普段、会社の売上や、テストの平均、いわゆる、百分率を使って、構成比等を算出している業務です。
たぶん、普通は、ここまでです。
基本統計量でやっていることは、母集団(抽出元:百位分数)のデータの中身をデータ分析することによって、推測できるようにします。
つまり、この母集団の状態を推測するには、正規分布を利用して推測するのが、一番適しています。
つまり
①百位分数
②基本統計量
やっていることは、同じようなことですが、統計の目的が違います。
ここは、本当に重要です。
とりわけ、Excelで統計を勉強しているなら、統計関数が、変わると、統計の目的も異なると思ってください。
S指数_4で、指数71の馬は全体のどこに位置するか?
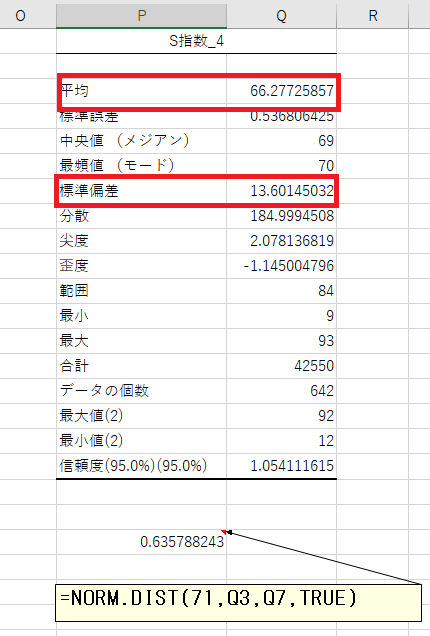
=NORM.DIST(71,Q3,Q7,TRUE)
NORM.DIST(ノーマルディストリビューション)関数で調べます。
そうすると、0.635、つまり、63.5%となります。
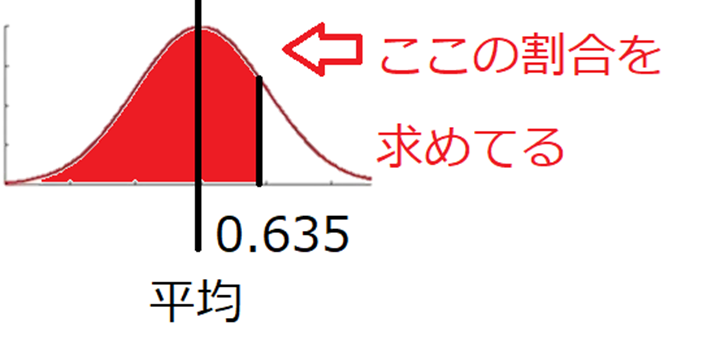
逆に、上位10%以内に入るためのS指数は、
=NORM.INV(0.9,Q3,Q7)となります。
つまり、84点の数字が必要となります。

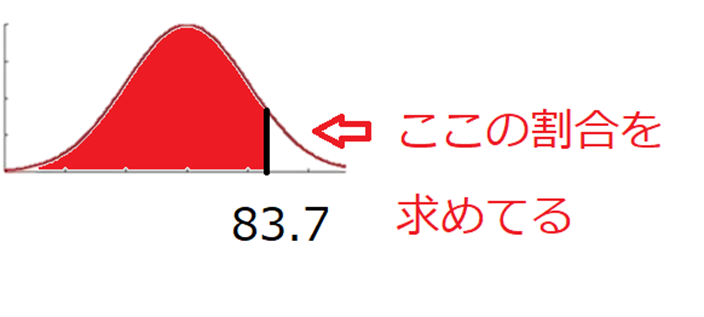
これが基本統計量を元に、母集団のデータを調べるということです。
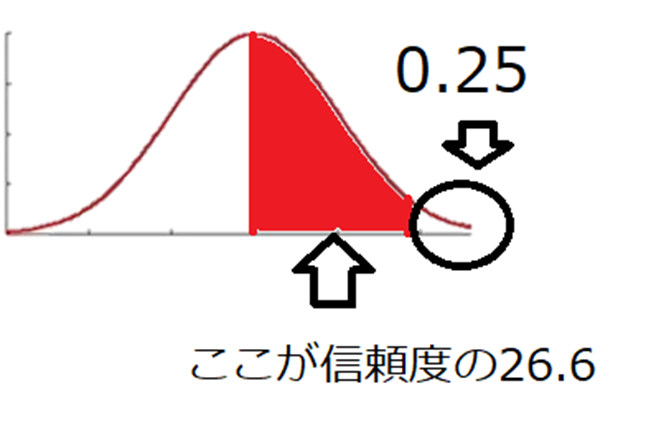
ちなみに、信頼度は、
=NORMINV(0.975,Q3,Q7)-Q3
これで求めることができます。
計算結果は、26.6となります。
ここがポイント

統計学は、仕切りが高そうに思いますが、用語を、確実に覚えると、それほど、難しいものではありません。もっとも、難しい分野もあります。それは、また、違う分析ツール等もあります。
まずは、Excelの分析ツールを使いこなしましょう。
まとめ
テータ分析ツールを利用することで、もっと、統計が好きになりました。
今後、重要な役割を担う学問だと思います。
今回のサンプルファイルは、ありません。

わからない事を延々と考えるのは、無駄です。
- なんで作動かないの?
- もうやだ!VBAなんか嫌い!
- ネットで調べても情報がない!
必ず作動するコードが、ここにあります。




















