目次
幾何学平均ってなに?
こんにちは。伊川(@naonaoke)です。
今回は、幾何学平均について紹介します。
幾何学平均というと、難しいかもしれません。
平均といっても色々な平均があります。
今回は、その点を重点的に説明します。
今回のブログはこんな人におすすめ
- Excelで統計を勉強したい人
- Excelの統計関数を勉強したい人
- 幾何学平均に興味のある人
このブログを読み終わるころには・・・
また、幾何学平均を理解することが出来ます。
平均にも色々ある
普通に平均というと、母数で合計を割ったものになります。
Excelの関数で言うならば、Averave関数になります。
Averave関数を、数学的にいうならば、相加平均といいます。
しかし、相加平均には、弱点があります。
幾何学平均 作業手順 その1 相加平均の弱点
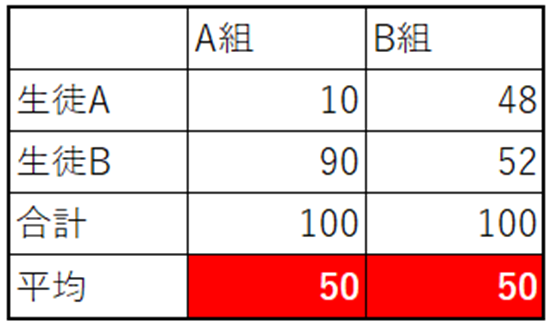
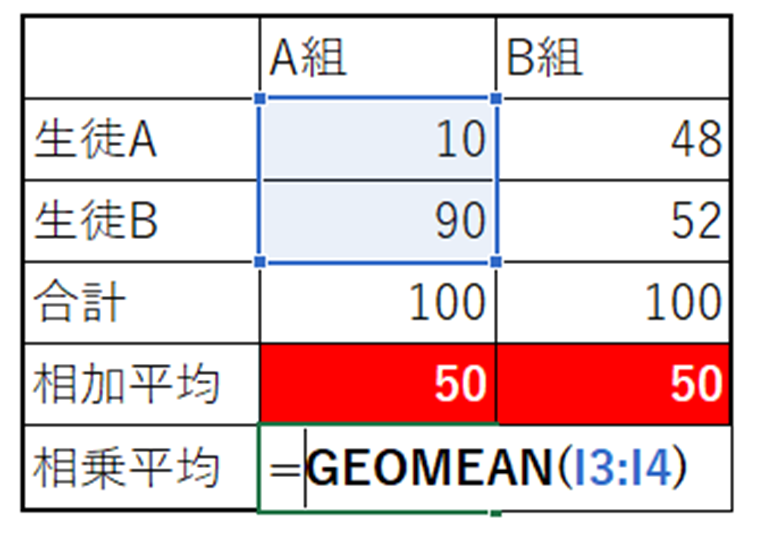
上の図を見てください。
A組とB組の平均点は、同じく50です。
しかし、この平均には、あまりにも無理があります。
B組の平均点50は、納得できますが、A組の平均点は、納得ができないです。
それは、A組の生徒Aと、生徒Bの点が、80点も離れているからです。
このように、相加平均(Averave関数)は、平均したい点数が、離れたら、離れるほど、数字がおかしくなります。
幾何学平均 作業手順 その2 GEOMEAN関数
平均したい点数、または、値が離れている場合は、相乗平均(GEOMEAN関数)を使います。
高校の数学で習ったはずですが、私には記憶にありません。
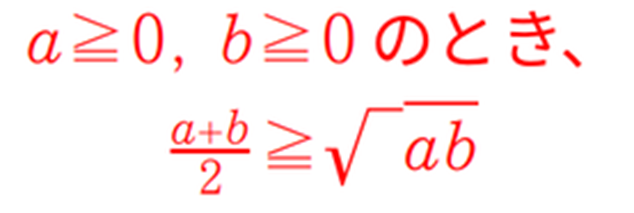
このような公式です。
しかし、この面倒な公式を GEOMEAN関数は一瞬で計算してくれるので、公式を覚えることは不要です。
どの場面で、相乗平均をつかうのか、相加平均を使うのかを覚えるのではなく、暗記しましょう。
幾何学平均 作業手順 その3 相乗平均を使う場面
- 経済成長率
- 人口増加率
- 売上増加率
問題
この3つを覚えておくと十分だと思います。
一例をあげます。
さらに、2020年いは、8倍になりました。
1年あたりの人口増加率は、何倍か?
正解は、実際には2倍のさらに8倍ですから、2×8=16倍にならなければいけません。
相加平均の場合
相加平均(Averave関数)⇒ (2+8)/2=5 5倍
1年あたり5倍になり、結果はおかしいとなります。
相乗平均の場合
しかし、相加平均(GEOMEAN関数)を利用すると、結果が違います。
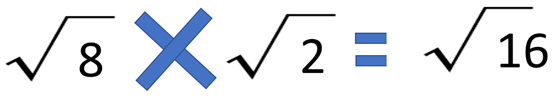
16の平方根は、4です。
つまり、1年目に4倍、2年目に4倍で、16倍となり、つじつまが合います。
相加率や、成長率の平均で使います。
幾何学平均 その4 A組と、B組の平均を、相乗平均で算出
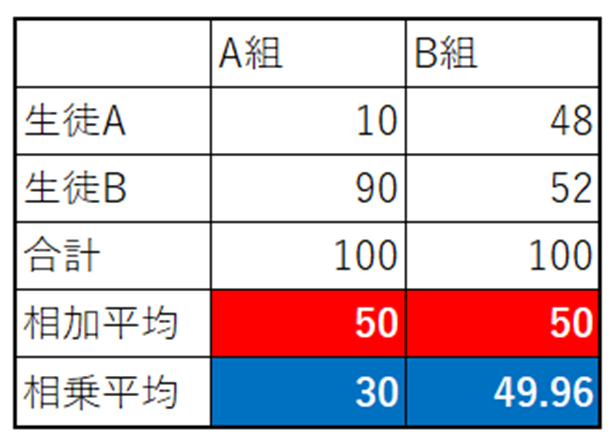
A組の相乗平均は、なぜ30になるのでしょうか?
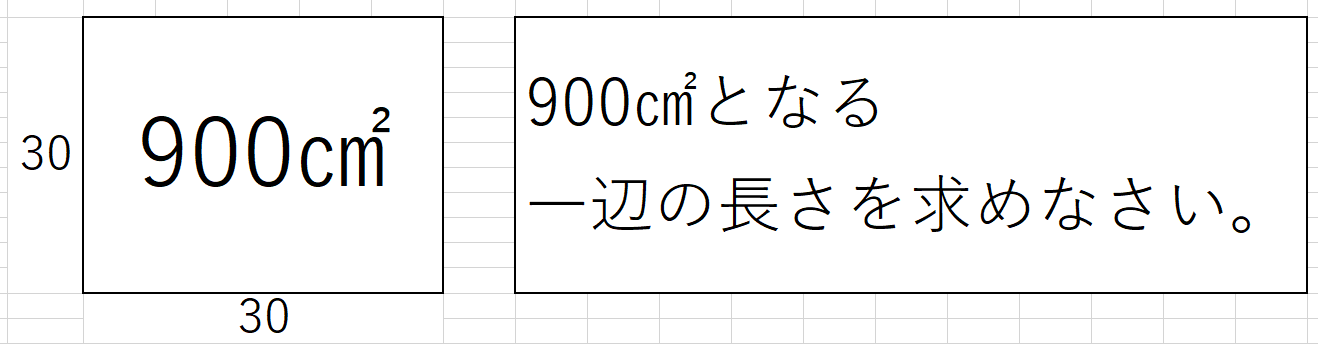
900㎠の1辺の長さは、普通の人は、1辺が、30㎝と答えるはずです。
20㎝と45㎝の組合を選択する人は、ほとんどいないと思います。
相乗平均が、幾何学平均といわれる所以になります。
誰しもが、選ぶ数字、この場合でしたら、30㎝です。
この30㎝を、一瞬で算出するのが、GEOMEAN関数なのです。
幾何学平均 その5 GOMEAN関数の使い方
セルに、GOMEANと入力後、対象のセルをなぞるだけです。
SUM関数と同じで特に難しい操作ではありません。
ここがポイント

統計に関しては、勉強していくと本当に面白いですね。複雑な計算も、Excelには、統計関数が完備されています。データ分析も楽しくなります。統計に関しては、関数や、VBAでなく、統計学そのものの考え方です。
まとめ
相乗平均を勉強してから、自社の平均の数字を疑うようになりました。
数字を提示されると、一見、正しいエビデンスに見えます。
しかし、エビデンスの根拠となる数字を疑うことを教えてくれるのが、統計学です。
最後まで、読んでいただきありがとうございました。
今回のサンプルファイルは、No176です。

わからない事を延々と考えるのは、無駄です。
- なんで作動かないの?
- もうやだ!VBAなんか嫌い!
- ネットで調べても情報がない!
必ず作動するコードが、ここにあります。
















