目次
営業成績予測する 回帰分析ってなに?
こんにちは。伊川(@naonaoke)です。
今回は回帰分析を紹介します。
言葉自体が、難しいので、わからないと投げ出す人が多いかもしれません。
しかし、この回帰分析は、1次関数が関わってきます。
y=ax+b
この公式を使います。
まさか、こんなところで、1次関数に出会うとは思いませんでした。
学問は、意外なところでリンクするものです。
このブログはこんな人にお勧め
- 回帰分析をExcelで表現したい人
- Excelで統計関数を勉強している人
- Excelで統計学を勉強している人
このブログを、読み終わるころには・・・・
回帰分析が理解できます。回帰分析のグラフもExcelを使って書けるようになります。SLOPE(スロープ)関数、INTERCEPT(インターセプト)関数が使えるようになります。
言葉自体に馴染みはないですが、そんなに難しくありません。
回帰分析とは
回帰とは、もともと、regression(リィグレェシャン)を由来にするそうです。
Y の増減によって、Xの値が決まるということです。
統計学においては、
Xを説明変数
Yを目的変数
このような呼び方をします。
カンタンにいうと、
yが1の時に、xがどのような値をとるのか?
yの値が決まったら、xの値も決まるので、
決まった値を通る直線を書いて、その係数aと、切片bを求めると予測ができるのではないか?
特に、中学では、係数aを変化の割合、切片bを、y切片と言いました。
中学で学ぶのは、速度と距離をグラフに書いた記憶があります。
では、今回は営業成績を題材にします。
回帰分析 作業手順 その1 データベースを各院
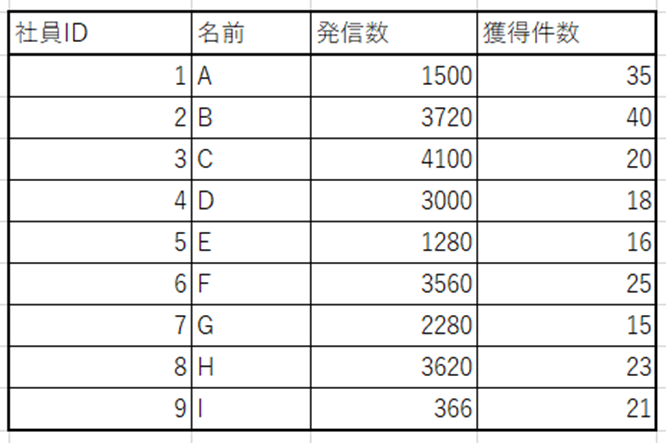
※発信数というのは、電話を掛けた回数です。
この表から考えると、Aさんは、1,500回電話を架けて、35件の獲得ということになります。
分析するのは、電話を架ければ、架けるほど、獲得できるのか?
つまり、発信数を向上させると、獲得件数は伸びるのか?
回帰分析を使って、分析をしたいと思います。
回帰分析 作業手順 その2 表からグラフを書いてみる
データを選択する
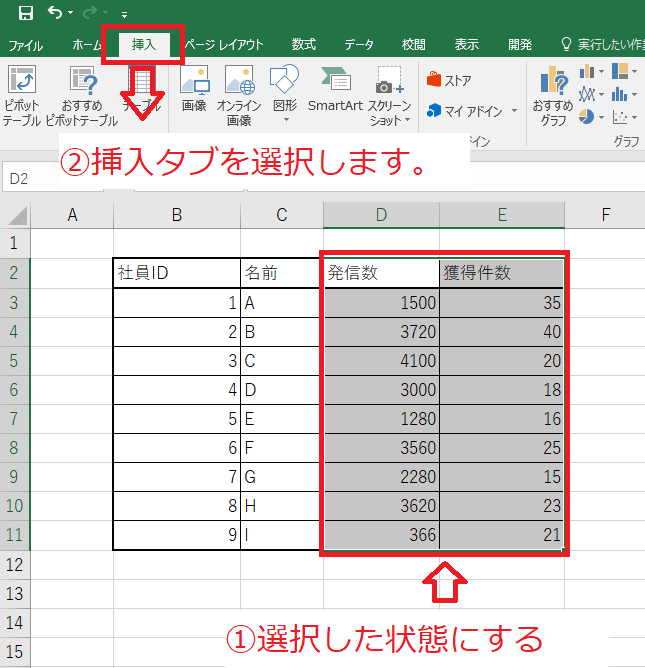
散布図を作成する
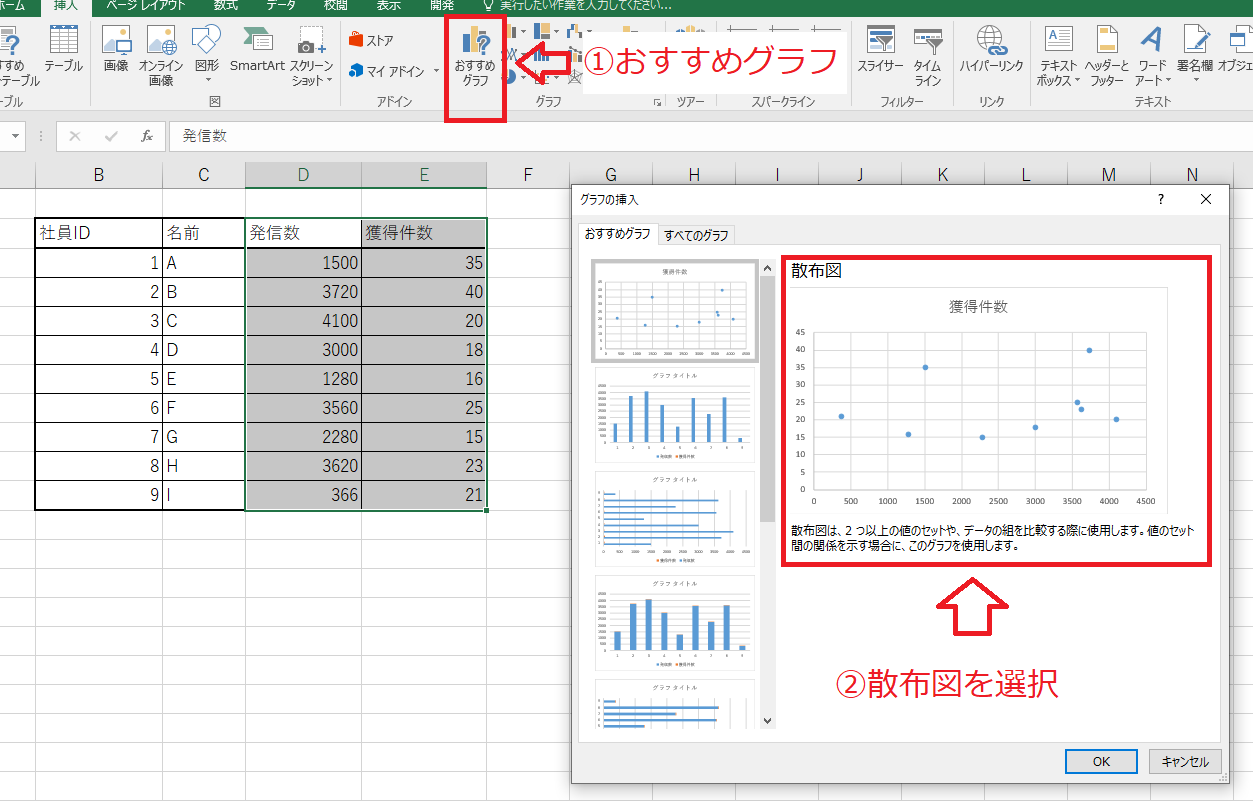
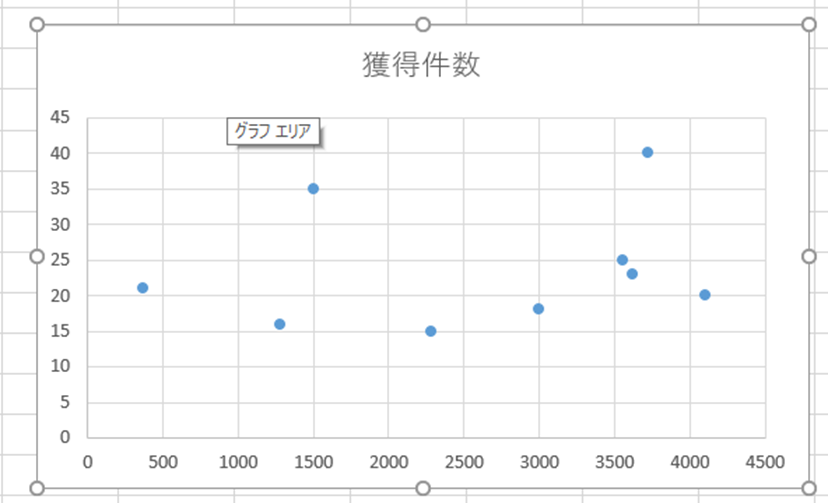
近似曲線を描く
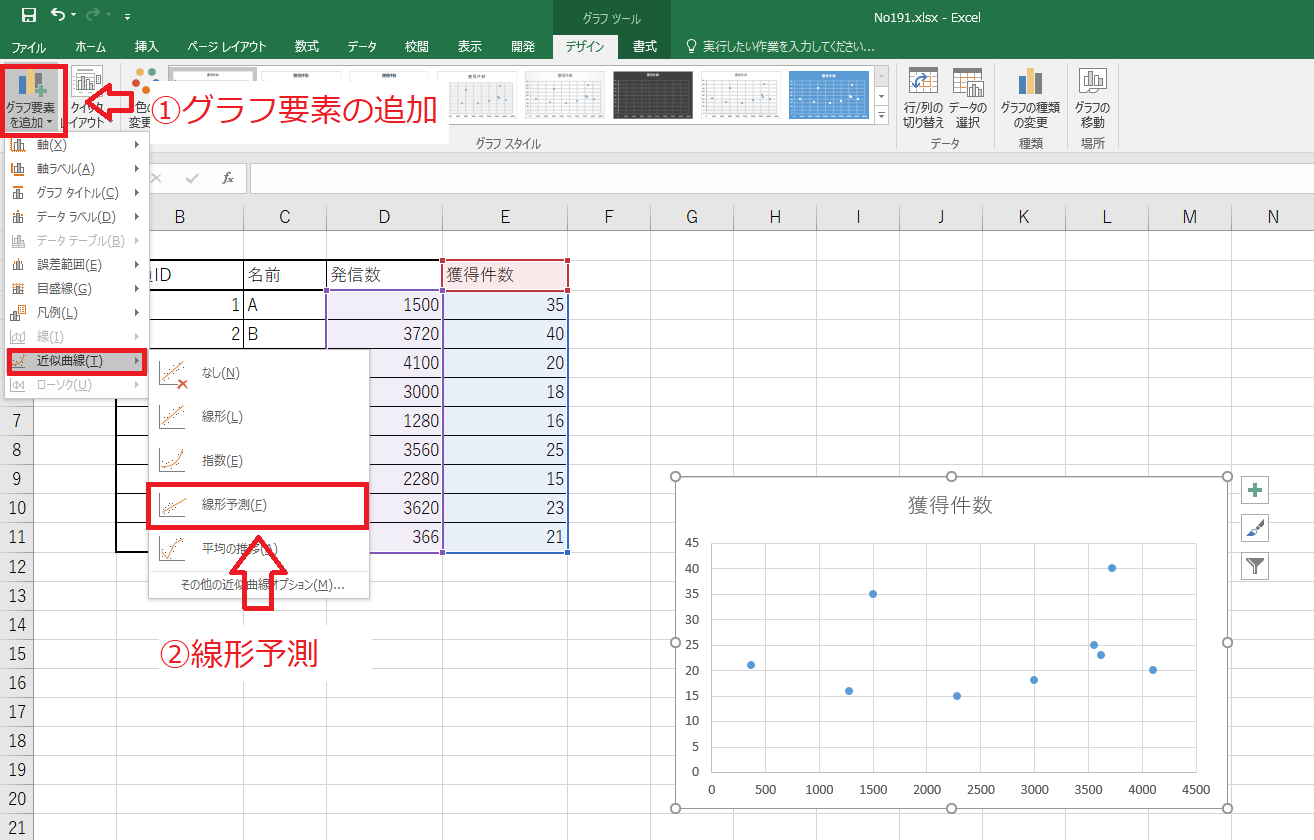
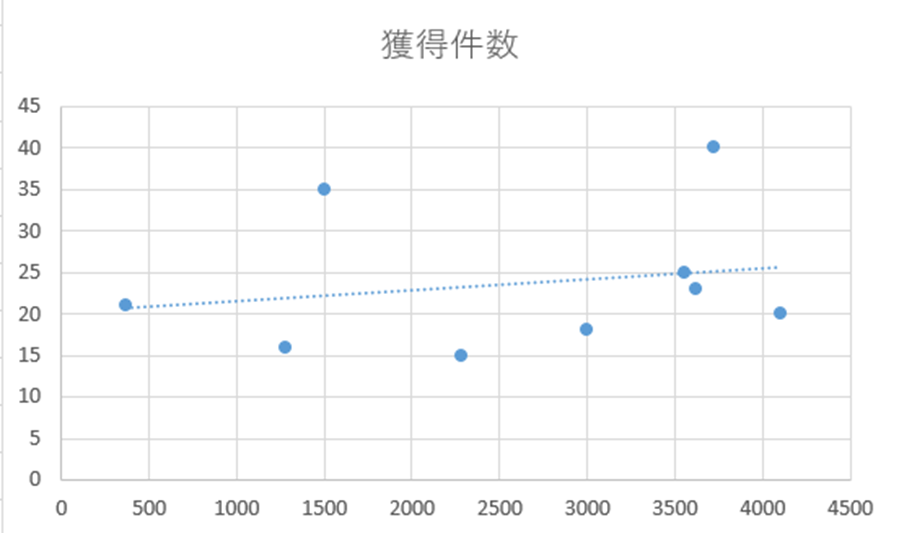
グラフを装飾する
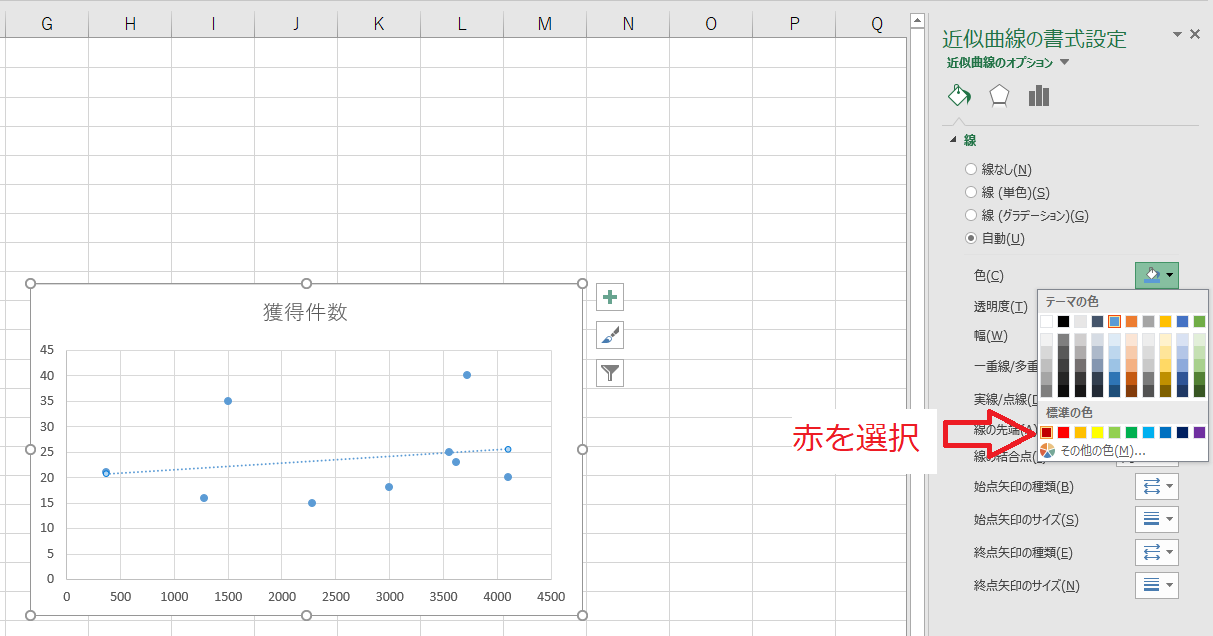
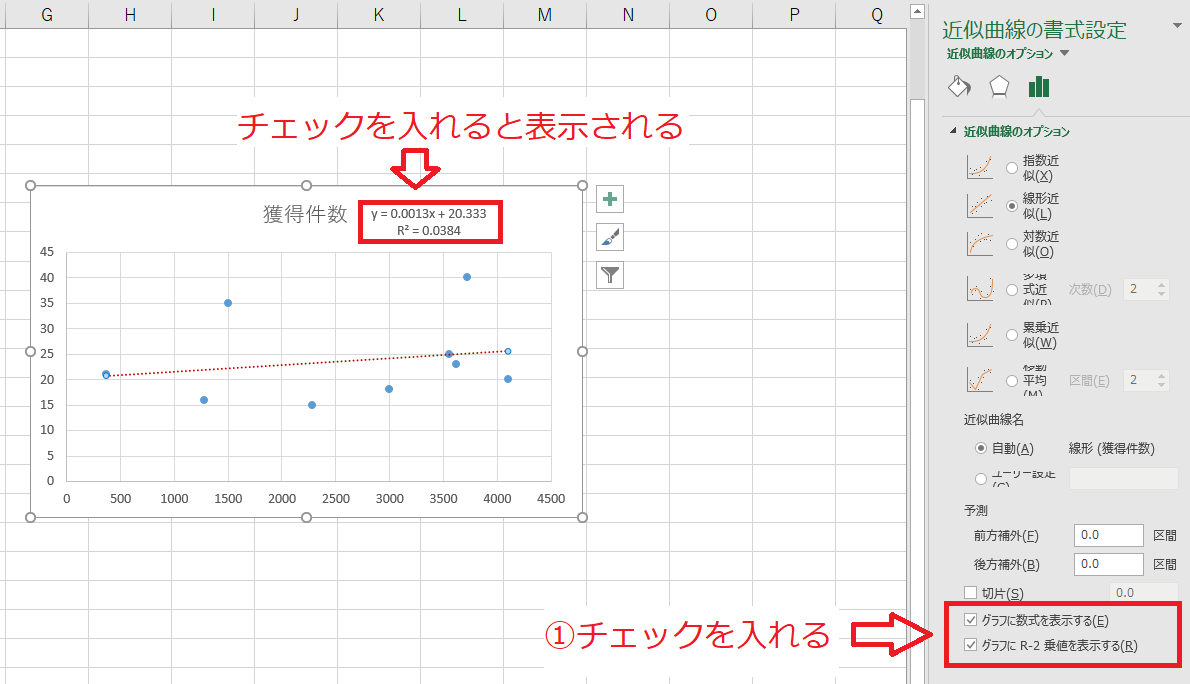
これでグラフは完成です。
回帰分析 作業手順 その3 関数で表現してみる
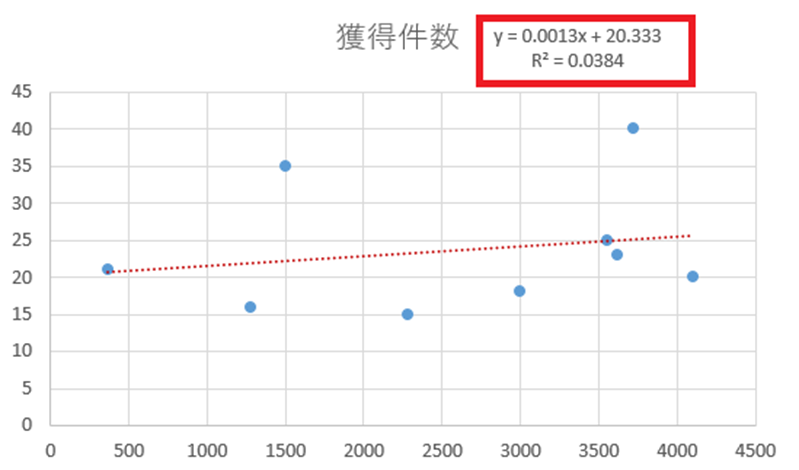
赤枠の部分を関数で表現してみます。
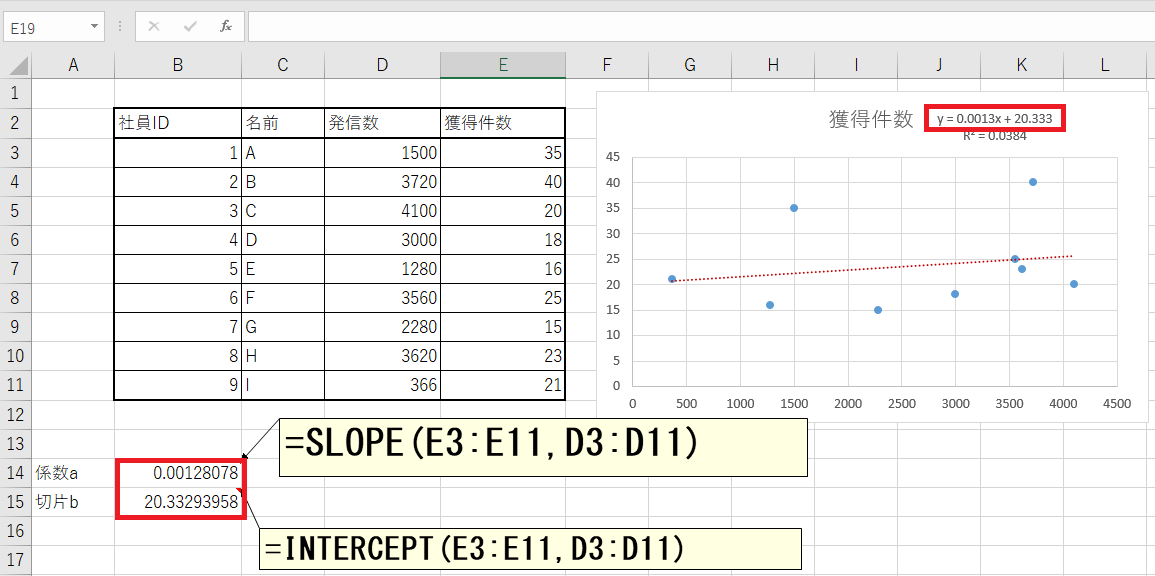
関数で表現すると、上の図のようになります。
回帰分析 作業手順 その4 営業予測をしてみる
SLOPE関数と、INTERCEPT関数で求めた結果で、営業予測をしてみます。
y= 0.00128078x+ 20.33293958
xは電話を架けた回数なので、1,000回電話を架けたら、どれくらいの獲得件数になるのでしょうか?
21.6件という結果になりました。
獲得件数の平均が、21.3件なので、平均より少し上という結果になりました。
ただし、実際にやってみなければ、わかりません。
回帰分析 作業手順 その5 回帰係数と相関係数
相関係数と回帰係数は違います。
相関係数は、-1~1の間に収まります。
しかし、回帰係数は‐1~1の間には収まりません。
また、今回は、発信数(電話を架けた回数)から、獲得件数を予測しました。
しかし、逆に、獲得件数から、発信数(電話を架けた回数)を予測することも可能です。
現時点では、相関係数と、回帰係数は違うということだけを覚えてください。
ここがポイント

今回は、回帰分析を紹介しました。厳密には、単回帰分析と言います。ということは、重回帰分析もあります。Xの説明関数は、今回は、発信数(電話を架けた回数)だけです。
Xの要素をもっと増やして、経験値、年齢等を増やすことができます。
そうすることによって、もっと複雑なデータ分析ができます。
まとめ
回帰分析を初めて読んだとき、理解ができませんでした。
しかし、自分が行っている業務に例えると理解ができました。
異なった数値で回帰分析・・・・・・・・
競馬にも使えそうです。
今回も最後まで読んでいただき、ありがとうございました。
今回のサンプルファイルは、No191です。

わからない事を延々と考えるのは、無駄です。
- なんで作動かないの?
- もうやだ!VBAなんか嫌い!
- ネットで調べても情報がない!
必ず作動するコードが、ここにあります。


















