競馬には、ハンデ戦というレースがあります。
このレースは、強い馬には、斤量(錘)を大きくします。
反対に、弱い馬には、斤量(錘)を軽くします。
この条件でレースをしたときの傾向を考えます。
使うのは、Excelの分析ツールにある、Z検定です。
目次
競馬の斤量についての一考 軽ハンデは有利なのか?
こんにちは。伊川(@naonaoke)です。
久しぶりに、Excelでデータ分析をしたいと思います。
今回は、思いっきりの競馬ネタです。
前半でも説明したように、競馬には、ハンデ戦なるレースがあります。
弱い馬でも勝てるように、斤量(錘)で馬の能力を調整します。
忘れていた頃に、本当に強い馬が、成績が思わしくなく、軽ハンデで、駆け抜け、万馬券を演出します。
この傾向について、競馬場で、違うのかを考えます。
このブログはこんな人にお勧め
- 競馬で検索して、この記事にたどり着いた人
- Excelを利用して競馬を研究している人
- Excelの統計分析ツールを利用してみたい人
このブログを、読み終わるころには・・・・
但し、軽ハンデの馬は、たまに大穴を演出します。
この場合は、別途、分析が必要とないますので、その分析は、別のブログで紹介します。
検定のフローチャート

このような図になります。
検定系は、この図が頭に入っていないといけません。
入っていないと、とりあえず、t検定になります。
t検定でも、間違いではありませんが、正確な検定をするためには、理解したほうがいいでしょう。
今回は、z検定をやります。
Z検定
Z検定を利用するには、結構厳格な基準があります。
母集団の平均と標準偏差がわかっていること
標本は、母集団からランダムに抽出されていること
母集団は、正規分布に従っていること
一般的には、母集団が初めからわかっているということは、まず、ありません。
なので、全国の学年別標準テストなどに、使います。
今回の母集団は下記の通りです。
東京競馬場と、中山競馬場において
芝1,600mのレース
ハンデ戦
帰無仮説は、東京競馬場と、中山競馬場のハンデ戦においては、1着になる馬は、斤量(錘)に関係がない。
このようになるでしょう。
Z検定 作業手順 その1 データベース確認
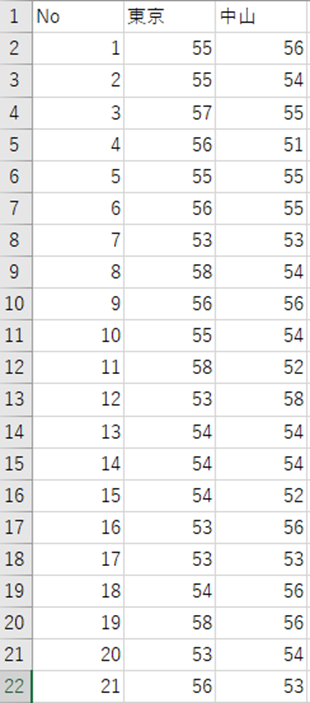
このようなデータベースになっています。
つまり、コール手前が坂になっているから、逆転が起こる可能性が高いです。
これを上りきると短い平坦部分を挟んだ下り勾配が続き、第4コーナーから上り勾配に転じます。
ゴールまでの直線には残り 480 m地点~260 m地点にかけて高低差 2 mの長い上り坂があり、「だんだら坂」とも呼ばれ東京競馬場の名物となっています。
直線は、約510mです。
Z検定 作業手順 その2 検定に必要な数値を算出する

この辺は、それほど難しくありません。
関数を知っていれば、利用方法は、SUM関数と変わりません。
Z検定 作業手順 その3 一応、正規分布に従っているか確認する

正規分布関数に指定した値を代入したときの確率を求めるには、NORM.DIST(ノーマル・ディストリビューション)関数を利用します。
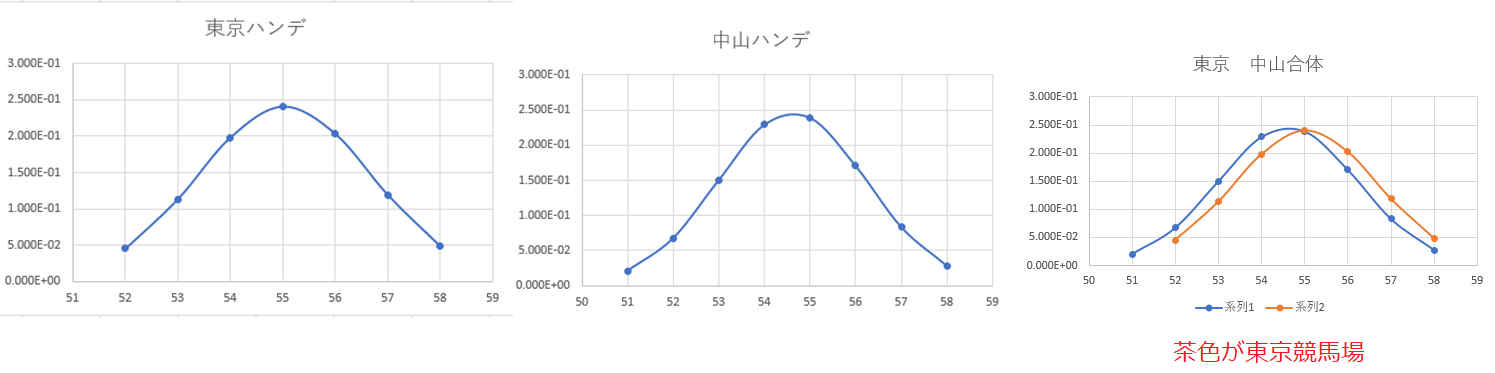
なんとなく、正規分布っぽくなりました。
今回は検定をするまでもなく、平均と、この正規分布を見る限り、斤量に関係がありません。
でも、Z検定の手順を紹介します。
Z検定 作業手順 その4 分析ツールを使う
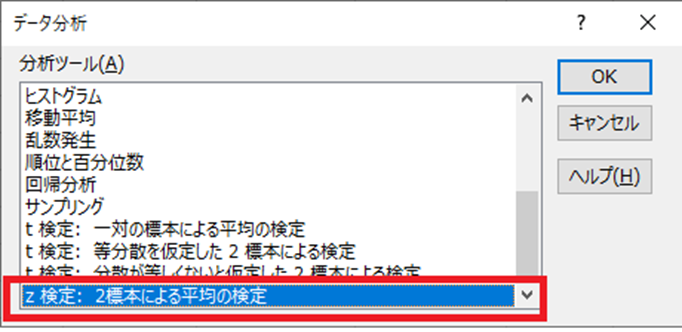


帰無仮説は、東京競馬場と、中山競馬場のハンデ戦においては、1着になる馬は、斤量(錘)に関係がない。
本当に関係がないので、東京競馬場と中山競馬場で行われるハンデ戦で、1着になる馬に関しては、斤量は関係がない。
つまり、帰無仮説は、棄却されないということがわかりました。

Z検定 作業手順 その5 片側検定、両側検定

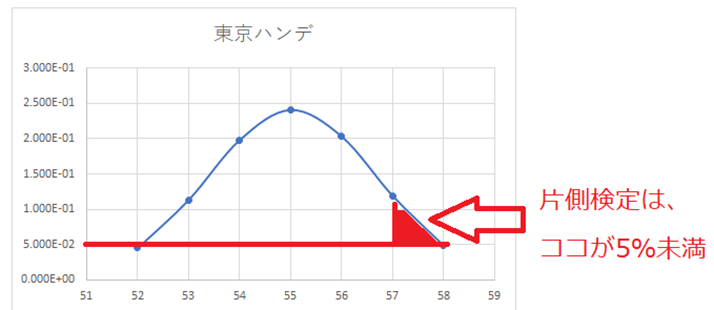

どちらも満たしていません。
両側検定は、単純に違いがあるのかを確認
片側検定は、どちらが大きいのかを確認
Z検定に関して、平均を見れば、どちらが大きいのかを確認できます。
Z検定に関しては、どちらが大きいのかを判断して、片側検定の有意差が、何%あるのかを確認しましょう。
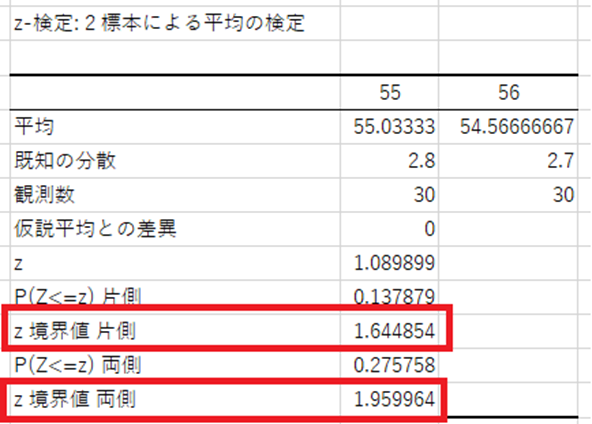
ここの意味合いに関しては、下記の通りです。
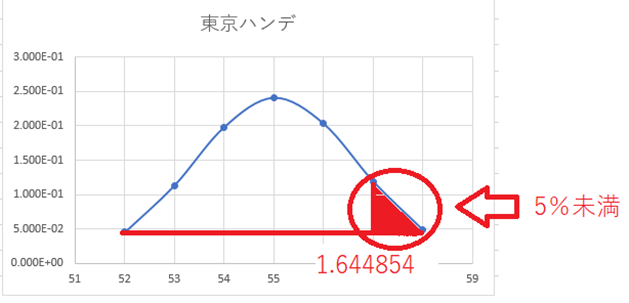
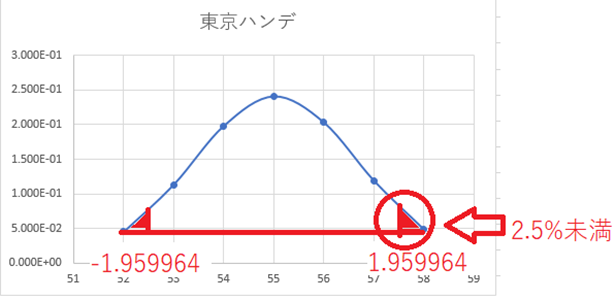
このようになります。
素朴な疑問だったこと
この5%未満等は、何を基準に行っているのかが、わかりませんでした。
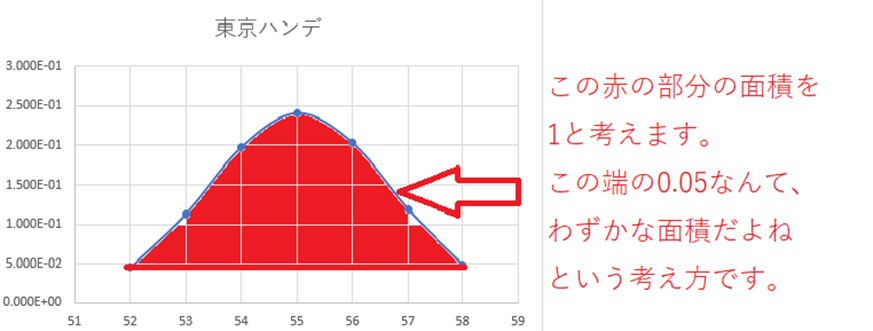
このわずかな面積が、有意差ということになります。

速度は一定ではないですが、その速度の差が、標準偏差となります。
面積を考えるという事は、数学では、結構、高度なことです。
図形をイメージすることは、右脳も使うことになりあます。
数学もイメージなんですね。
ここがポイント

違う検定方法でも、試していますが、有意差が、5%未満になることは、競馬では滅多にありません。
たぶん、データ抽出方法にも問題はあると思います。
あなたの会社では、このような検定はしていますか?
やりたいことを実現するのが、VBA、関数であるなら、そのデータをもとに、経営分析をするのが統計です。
貸したお金が返しましょうというのは、だれでも知っています。
もちろん民法にも書いています。
しかし、貸したお金をどのような手続きで、相手から返金させるのかというのは、民事訴訟法になります。
まず、民事訴訟法は、一般の人は知りません。
統計や、マーケティングは、VBAよりも重要なものだと私は思います。
そう、民事訴訟法のように、返金を実現させるという意味で、統計分析は、未来のあなたの像を的確に映してくれます。
まとめ
今回の分析は有意差がありませんでしたが、ここでくじけるわけにはいきません。
基本を勉強すれば、何にでも、応用が利きます。
そう、クエリのように、何にでも変幻自在に、知識を利用することができます。
今回も最後まで読んでいただき、ありがとうございました。
今回のサンプルファイルは、No233です。

わからない事を延々と考えるのは、無駄です。
- なんで作動かないの?
- もうやだ!VBAなんか嫌い!
- ネットで調べても情報がない!
必ず作動するコードが、ここにあります。


















