電話セールスは、迷惑電話としてお叱りを受けることもあります。
しかし、電話セールスは、お客様に電話をすれば、するほど、契約が獲得できるのでしょうか?
電話回数と、契約の獲得を統計学で証明をしたいと思います。
目次
電話セールスは、電話回数で、契約獲得できる?
こんにちは。伊川(@naonaoke)です。
以前にも同じことをやりました。
回帰分析と、重回帰分析です。
その時は、相関関係があるのか、ないのか?
それをグラフで表しました。
しかし、根拠のある判断をするには、検定が必要となります。
前回の記事と合わせて読んでいただくと理解が深まると思います。
今回の表は、前回の表とは少し違っています。
数字を変えることで、出来れば、実際に計算をしてほしいと思ったからです。
難しいかもしれませんが、計算はExcelがやってくれますので、手順を覚えてください。
このブログはこんな人にお勧め
- Excelで統計を勉強したい人
- Excelで統計関数を勉強している人
- 統計学に興味のある人
このブログを、読み終わるころには・・・・
前回の記事では、単純に数字を出しましたが、検定を使うことで、より、信頼性を担保できます。少し、難しい言葉も出てきますが、出来るだけわかりやすく解説をしたつもりです。
無相関検定
今回の検定は、相関関係がないということを証明します。
前回は、相関関係があるということを証明しました。
今回の証明は下記の通りになります。
帰無仮説⇒相関関係はない。
無相関検定 その1 検定統計量
この言葉を理解するのに時間がかかりました。
一旦、ここで詳しく解説をします。
そもそも検定とは、検定統計量を求めて、その値が、棄却域にあるか、無いかを調べます。
検定統計量とは統計学的仮説検定に用いる統計量のことです。
統計学的仮説検定ですが、これは2つ以上のグループのデータの間に差があるかどうかをみるものです。
つまり、統計は、推測でしかありません、
ここなのですが、起きた現象が、5%以上なら、差があっても、偶然として、処理します。
だから、実は、差はない(偶然に起きた現象)というのが、帰無仮説なのです。
統計学は、推測から、実際に起きることの確率を証明したいわけですから、
偶然に発生した現象となっては困ります。
だらか、差はないというのが、帰無仮説になります。
コインを投げて、裏が出るが、表が出るか判定する
コインを6回投げて、すべて表が出たとします。
表が出る確率は、1/2です。
1/2×1/2×1/2×1/2×1/2×1/2 =1/64 = 約1.5%です。
そうすると、帰無仮説は棄却されます。
表が出やすいコインとい結論になります。
このような検定に使われるデータ、つまり、表6回裏0回が、検定統計量となります。
無相関検定 作業手順 その2 検定統計量で抑えるべきこと
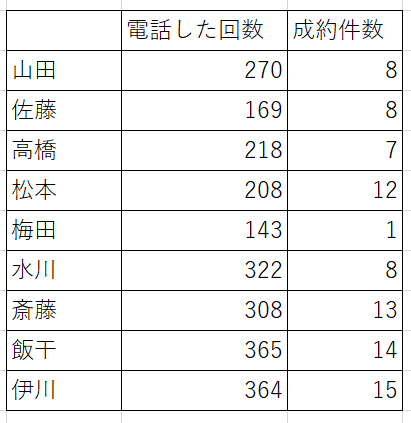
前回の表とは少し違いますが、上記の表で検証してみましょう。
帰無仮説は、電話した回数と成約件数の増減は、関係がないとなります。(2つの変量に関係がない)
実際に難しいのは、検定統計量の計算式です。公式は、記載しません。
そして、検定統計量は、n-2のt分布に従うということです。
今回のnは、成約件数になります。
無相関検定 作業手順 その3 各数値を求める
nを求める
今回のnは成約件数です。

相関係数を求める
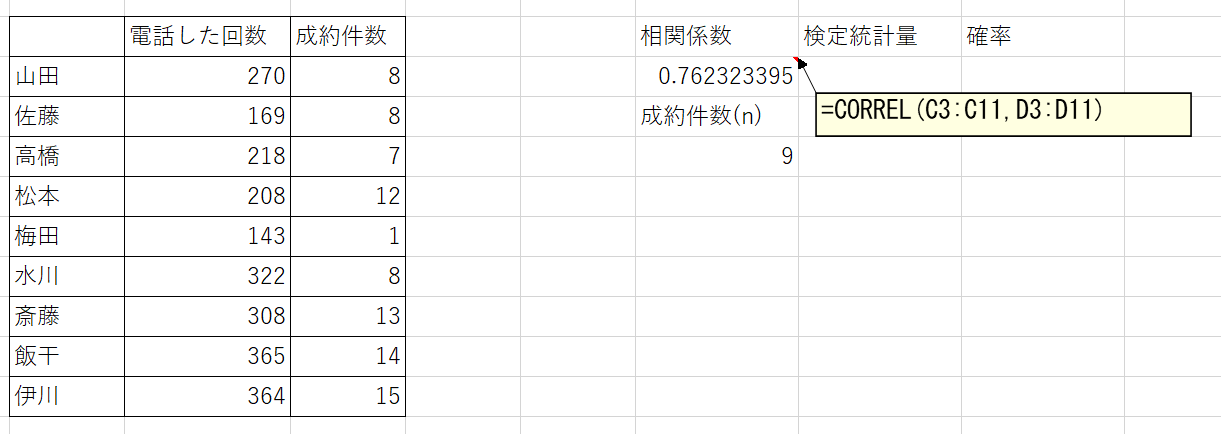
検定統計量を求める
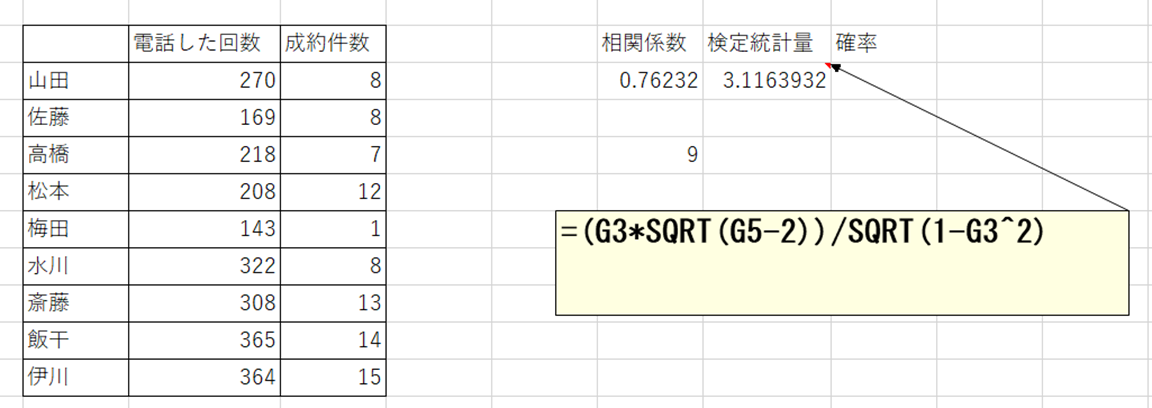
ここの計算がたぶん一番難しいです。
相関係数にn-2を2乗を、1から相関係数の2乗で割るのです。
なぜ、セルG5から、2を引くのかというと、検定統計量は、n-2のt分布に従うからです。
nは成約件数なので、nつまり、セルG5から、2を引くのです。
無相関検定 作業手順 その4 関数で確率を求める
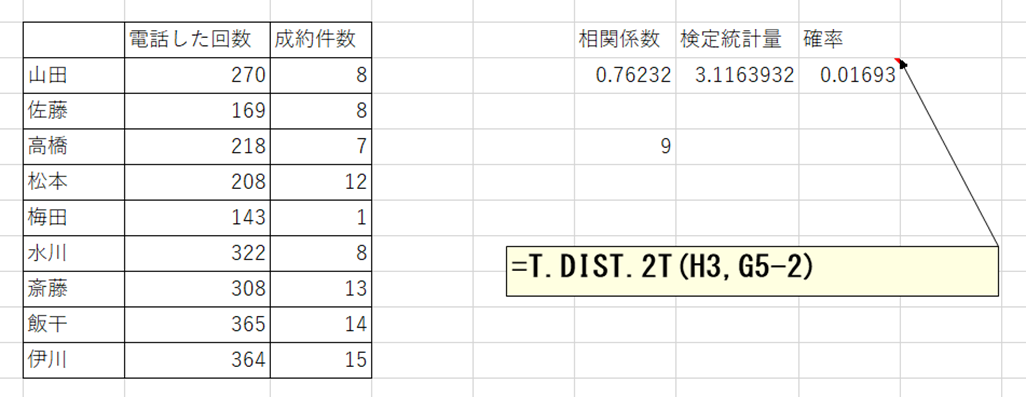
T.DIST.2T(ティー・ディストリビューション・ツー・テイルド)関数は、t分布の両側確率を求めます。
特に、セルG5-2のことを自由度と言います。
確率は、1%以下ではないので、無相関ではないとは、言えないというような結論でしょう。
無相関検定 番外編 自由度ってなに?
カンタンに言うと、自由に決めることができる数字や、値です。
3つ数字を組み合わせて、10という値を作ります。
3+5+2=10
3と5は自由に決めることができます。
しかし、2は自由に決めたわけではありません。
強制的に2を入れないと、10にはなりません。
これが、自由度です。
不変分散の時に、なぜ、n-1で割るのかを考えてもわかりませんでしたが、
この理屈で理解できた気がします。
この3つの数字を、nとするなら、nのうち2は自由に決めることができますが、1は強制的に決まります。
だから、nから、1を引くのです。
ここがポイント

今回は、自由度、検定統計量など、難しい言葉が出てきましたが、そういうものとして覚えてください。また、相関関係を積極的に証明するのはなく、あえて無相関と仮説を立てて、証明するという方法を紹介しました。難しい計算はExcelがやってくれるので、手順を覚えてください。
まとめ
この辺の知識がついてくると、早く競馬に使ってみたいという気持ちを抑えることができないです。
もっと、勉強して、競馬に使えるように頑張ります。
今回も最後まで読んでいただきありがとうございました。
今回のサンプルファイルは、No214です。

わからない事を延々と考えるのは、無駄です。
- なんで作動かないの?
- もうやだ!VBAなんか嫌い!
- ネットで調べても情報がない!
必ず作動するコードが、ここにあります。





























